The Speed of Gravity – What the Experiments Say

Tom Van Flandern

Meta Research

<tomvf@metaresearch.org>

[as published in Physics Letters A 250:1-11 (1998)]

Abstract. Standard experimental techniques exist to determine the propagation speed of forces. When we apply these techniques to gravity, they all yield propagation speeds too great to measure, substantially faster than lightspeed. This is because gravity, in contrast to light, has no detectable aberration or propagation delay for its action, even for cases (such as binary pulsars) where sources of gravity accelerate significantly during the light time from source to target. By contrast, the finite propagation speed of light causes radiation pressure forces to have a non-radial component causing orbits to decay (the “Poynting-Robertson effect”); but gravity has no counterpart force proportional to to first order. General relativity (GR) explains these features by suggesting that gravitation (unlike electromagnetic forces) is a pure geometric effect of curved space-time, not a force of nature that propagates. Gravitational radiation, which surely does propagate at lightspeed but is a fifth order effect in , is too small to play a role in explaining this difference in behavior between gravity and ordinary forces of nature. Problems with the causality principle also exist for GR in this connection, such as explaining how the external fields between binary black holes manage to continually update without benefit of communication with the masses hidden behind event horizons. These causality problems would be solved without any change to the mathematical formalism of GR, but only to its interpretation, if gravity is once again taken to be a propagating force of nature in flat space-time with the propagation speed indicated by observational evidence and experiments: not less than 2x10¹⁰ c. Such a change of perspective requires no change in the assumed character of gravitational radiation or its lightspeed propagation. Although faster-than-light force propagation speeds do violate Einstein special relativity (SR), they are in accord with Lorentzian relativity, which has never been experimentally distinguished from SR—at least, not in favor of SR. Indeed, far from upsetting much of current physics, the main changes induced by this new perspective are beneficial to areas where physics has been struggling, such as explaining experimental evidence for non-locality in quantum physics, the dark matter issue in cosmology, and the possible unification of forces. Recognition of a faster-than-lightspeed propagation of gravity, as indicated by all existing experimental evidence, may be the key to taking conventional physics to the next plateau.

Introduction

The most amazing thing I was taught as a graduate student of celestial mechanics at Yale in the 1960s was that all gravitational interactions between bodies in all dynamical systems had to be taken as instantaneous. This seemed unacceptable on two counts. In the first place, it seemed to be a form of “action at a distance”. Perhaps no one has so elegantly expressed the objection to such a concept better than Sir Isaac Newton: “That one body may act upon another at a distance through a vacuum, without the mediation of any thing else, by and through which their action and force may be conveyed from one to the other, is to me so great an absurdity, that I believe no man who has in philosophical matters a competent faculty of thinking, can ever fall into it.” (See Hoffman, 1983.) But mediation requires propagation, and finite bodies should be incapable of propagation at infinite speeds since that would require infinite energy. So instantaneous gravity seemed to have an element of magic to it.

The second objection was that we had all been taught that Einstein’s special relativity (SR), an experimentally well-established theory, proved that nothing could propagate in forward time at a speed greater than that of light in a vacuum. Indeed, as astronomers we were taught to calculate orbits using instantaneous forces; then extract the position of some body along its orbit at a time of interest, and calculate where that position would appear as seen from Earth by allowing for the finite propagation speed of light from there to here. It seemed incongruous to allow for the finite speed of light from the body to the Earth, but to take the effect of Earth’s gravity on that same body as propagating from here to there instantaneously. Yet that was the required procedure to get the correct answers.

These objections were certainly not new when I raised them. They have been raised and answered thousands of times in dozens of different ways over the years since general relativity (GR) was set forth in 1916. Even today in discussions of gravity in USENET newsgroups on the Internet, the most frequently asked question and debated topic is “What is the speed of gravity?” It is only heard less often in the classroom because many teachers and most textbooks head off the question by hastily assuring students that gravitational waves propagate at the speed of light, leaving the firm impression, whether intended or not, that the question of gravity’s propagation speed has already been answered.

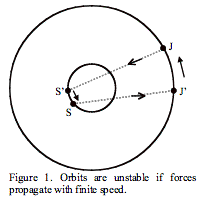Yet, anyone with a computer and orbit computation or numerical integration software can verify the consequences of introducing a delay into gravitational interactions. The effect on computed orbits is usually disastrous because conservation of angular momentum is destroyed. Expressed less technically by Sir Arthur Eddington, this means: “If the Sun attracts Jupiter towards its present position S, and Jupiter attracts the Sun towards its present position J, the two forces are in the same line and balance. But if the Sun attracts Jupiter toward its previous position S’, and Jupiter attracts the Sun towards its previous position J’, when the force of attraction started out to cross the gulf, then the two forces give a couple. This couple will tend to increase the angular momentum of the system, and, acting cumulatively, will soon cause an appreciable change of period, disagreeing with observations if the speed is at all comparable with that of light.” (Eddington, 1920, p. 94) See Figure 1.

Indeed, it is widely accepted, even if less widely known, that the speed of gravity in Newton’s Universal Law is unconditionally infinite. (E.g., Misner et al., 1973, p. 177) This is usually not mentioned in proximity to the statement that GR reduces to Newtonian gravity in the low-velocity, weak-field limit because of the obvious question it begs about how that can be true if the propagation speed in one model is the speed of light, and in the other model it is infinite.

The same dilemma comes up in many guises: Why do photons from the Sun travel in directions that are not parallel to the direction of Earth’s gravitational acceleration toward the Sun? Why do total eclipses of the Sun by the Moon reach maximum eclipse about 40 seconds before the Sun and Moon’s gravitational forces align? How do binary pulsars anticipate each other’s future position, velocity, and acceleration faster than the light time between them would allow? How can black holes have gravity when nothing can get out because escape speed is greater than the speed of light?

Herein we will examine the experimental evidence bearing on the issue of the speed of propagation of gravity. By gravity, we mean the gravitational “force” from some source body. By force, we mean that which gives rise to the acceleration of target bodies through space. [Note: Orbiting bodies do accelerate through space even if gravity is geometry and not a true force. For example, one spacecraft following another in the same orbit can stretch a tether between the two. The taut tether then describes a straight line, and the path of both spacecraft will be curved with respect to it.] We will examine the explanations offered by GR for these phenomena. And we will confront the dilemma that remains when we are through: whether to give up our existing interpretation of GR, or the principle of causality.

Propagation Delay versus Aberration

To understand how propagation speeds of phenomena are normally measured, it will be useful to discuss propagation or transit delay and aberration, and the distinction between them. The points in this section are illustrated in Figure 2.

In the top half of the figure, we consider the view from the source. A fixed source body on the left (for example, the Sun) sends a projectile (the arrow, which could also be a photon) toward a moving target (for example, the Earth). Infinitely far to the right are shown a bright (large, 5-pointed) star and a faint (small, 4-pointed) star, present to define directions in space. Because of transit delay, in order to hit the target, the source body must send the projectile when it is seen in the direction of the faint star, but send it toward the direction of the bright star, leading the target. The tangent of the lead angle (the angle between the two stars) is the ratio of the tangential target speed to the radial projectile speed. For small angles, this ratio equals the lead angle in radians.

In the bottom half of the figure, we consider the view from the target, which will consider itself at rest and the source moving. By the principle of relativity, this view is just as valid since no experiment can determine which of two bodies in uniform, linear relative motion is “really moving” and which is not. The projectile will be seen to approach from the retarded position of the source, which is the spatial direction headed toward the faint star. The angle between the true and retarded positions of the source, which equals the angle between the two stars, is called “aberration”. It will readily be recognized as the same angle defined in the first view due to transit delay.

Indeed, that is generally true: The initial and final positions of the target as viewed from the source differ by the motion of the target during the transit delay of the projectile. The same difference between initial and final positions of the source as viewed from the target is called the angle of aberration. Expressed in angular form, both are equal, and are manifestations of the finite propagation speed of the projectile as viewed from different frames. So the most basic way to measure the speed of propagation of any entity, whether particle or wave or dual entity or neither, is to measure transit delay, or equivalently, the angle of aberration.

Fact: Gravity Has No Aberration

1. The effect of aberration on orbits is not seen

As viewed from the Earth’s frame, light from the Sun has aberration. Light requires about 8.3 minutes to arrive from the Sun, during which time the Sun seems to move through an angle of 20 arc seconds. The arriving sunlight shows us where the Sun was 8.3 minutes ago. The true, instantaneous position of the Sun is about 20 arc seconds east of its visible position, and we will see the Sun in its true present position about 8.3 minutes into the future. In the same way, star positions are displaced from their yearly average position by up to 20 arc seconds, depending on the relative direction of the Earth’s motion around the Sun. This well-known phenomenon is classical aberration, and was discovered by the astronomer Bradley in 1728.

Orbit computations must use true, instantaneous positions of all masses when computing accelerations due to gravity for the reason given by Eddington. When orbits are complete, the visible position of any mass can be computed by allowing for the delay of light traveling from that mass to Earth. This difference between true and apparent positions of bodies is not merely an optical illusion, but is a physical difference due to transit delay that can alter an observer’s momentum. For example, small bodies such as dust particles in circular orbit around the Sun experience a mostly radial force due to the radiation pressure of sunlight. But because of the finite speed of light, a portion of that radial force acts in a transverse direction, like a drag, slowing the orbital speed of the dust particles and causing them to eventually spiral into the Sun. This phenomenon is known as the Poynting-Robertson effect.

If gravity were a simple force that propagated outward from the Sun at the speed of light, as radiation pressure does, its mostly radial effect would also have a small transverse component because of the motion of the target. Analogous to the Poynting-Robertson effect, the magnitude of that tangential force acting on the Earth would be 0.0001 of the Sun’s radial force, which is the ratio of the Earth’s orbital speed (30 km/s) to the speed of this hypothetical force of gravity moving at light-speed (300,000 km/s). It would act continuously, but would tend to speed the Earth up rather than slow it down because gravity is attractive and radiation pressure is repulsive. Nonetheless, the net effect of such a force would be to double the Earth’s distance from the Sun in 1200 years. There can be no doubt from astronomical observations that no such force is acting. The computation using the instantaneous positions of Sun and Earth is the correct one. The computation using retarded positions is in conflict with observations. From the absence of such an effect, Laplace set a lower limit to the speed of propagation of classical gravity of about 10⁸ c, where c is the speed of light. (Laplace, 1825, pp. 642-645 of translation)

In the general case, let be the speed of propagation of gravitational force, and let be the initial semi-major axis at time of an orbiting body in a system where the product of the gravitational constant and the total system mass is . Then the following formula, derived from the ordinary perturbation formulas of celestial mechanics (e.g., Danby, 1988, p. 327), allows us to compute the semi-major axis at any other time :

[1]

We will use this formula later to set limits on .

2. Gravity and light do not act in parallel directions

There is no cause to doubt that photons arriving now from the Sun left 8.3 minutes ago, and arrive at Earth from the direction against the sky that the Sun occupied that long ago. But the analogous situation for gravity is less obvious, and we must always be careful not to mix in the consequences of light propagation delays. Another way (besides aberration) to represent what gravity is doing is to measure the acceleration vector for the Earth’s motion, and ask if it is parallel to the direction of the arriving photons. If it is, that would argue that gravity propagated to Earth with the same speed as light; and conversely.

Such measurements of Earth’s acceleration through space are now easy to make using precise timing data from stable pulsars in various directions on the sky. Any movement of the Earth in any direction is immediately reflected in a decreased delay in the time of arrival of pulses toward that direction, and an increased delay toward the opposite direction. In principle, Earth’s orbit could be determined from pulsar timings alone. In practice, the orbit determined from planetary radar ranging data is checked with pulsar timing data and found consistent with it to very high precision.

How then does the direction of Earth’s acceleration compare with the direction of the visible Sun? By direct calculation from geometric ephemerides fitted to such observations, such as those published by the U.S. Naval Observatory or the Development Ephemerides of the Jet Propulsion Laboratory, the Earth accelerates toward a point 20 arc seconds in front of the visible Sun, where the Sun will appear to be in 8.3 minutes. In other words, the acceleration now is toward the true, instantaneous direction of the Sun now, and is not parallel to the direction of the arriving solar photons now. This is additional evidence that forces from electromagnetic radiation pressure and from gravity do not have the same propagation speed.

3. The solar eclipse test

Yet another manifestation of the difference between the propagation speeds of gravity and light can be seen in the case of solar eclipses (Van Flandern, 1993, pp. 49-50). The Moon, being relatively nearby and sharing the Earth’s 30 km/s orbital motion around the Sun, has relatively little aberration (0.7 arc seconds, due to the Moon’s 1 km/s orbital speed around Earth). The Sun, as mentioned earlier, has an aberration of just over 20 arc seconds. It takes the Moon about 38 seconds of time to move 20 arc seconds on the sky relative to the Sun. Since the observed times of eclipses of the Sun by the Moon agree with predicted times to within a couple of seconds, we can use the orbits of the Sun and the Moon near times of maximum solar eclipse to compare the time of predicted gravitational maximum with the time of visible maximum eclipse.

In practice, the maximum gravitational perturbation by the Sun on the orbit of the Moon near eclipses may be taken as the time when the lunar and solar longitudes are equal. Details of the procedure are provided in the reference cited. We find that maximum eclipse occurs roughly 38±1.9 seconds of time, on average, before the time of gravity maximum. If gravity is a propagating force, this 3-body (Sun-Moon-Earth) test implies that gravity propagates at least 20 times faster than light.

Electromagnetic Analogies and Gravitational Radiation

1. Myth: Gravity from an accelerating source experiences light-time delay

In electromagnetism, it is said that moving charges anticipate each other’s linear motion, but not acceleration, and that acceleration causes the emission of photons. If gravity behaved in an analogous way, moving masses would anticipate each other’s linear motion, but not acceleration, and accelerating masses would emit gravitational radiation. Indeed, the orbit of binary pulsar PSR1913+16 is observed to slowly decay at a rate close to that predicted by GR from the emission of gravitational radiation. Could that be evidence for changes in gravity propagating at lightspeed?

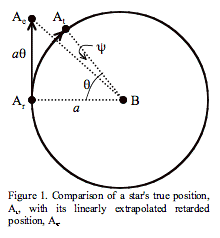
First, we will calculate the acceleration predicted for any two stars if each star responds to the linearly extrapolated retarded position and velocity, but not acceleration, of its companion over one light time between the stars. This would be consistent with the electromagnetic analogy. In Figure 3, we will consider the orbit of component A relative to component B during the light time between the two stars. We will then consider three positions of component A: its true, instantaneous position, A_t; its retarded position one light time ago, A_r; and its linearly extrapolated position one light time ahead from its retarded position, A_e. As before, let the product of the gravitational constant and the total system mass be , and the radius of A’s circular orbit around B be . Also let the speed of light be , and A’s orbital period be . Finally, is the angle at B through which A moves during the light time , and is the angle at B between A_e and A_t. By construction, the linear distance from A_r to A_e is equal to the length of the arc from A_r to A_t, and both are equal to .

The difference in the distance of A_e and A_t from B causes only small, non-cumulative effects on the orbit. However, the angle causes the extrapolated retarded position to feel a transverse force component that continually increases the orbital period . From the triangles in the figure we see that . Since is normally a very small angle, we can expand the arctangent into a series and retain only significant terms. The result is . However, is times the light time, or . So the transverse perturbing acceleration , which is times the radial orbital acceleration , can be found from . Finally, from (Danby, 1988, p. 327) and with some minor change of variables and simplification, we arrive at:

[2]

Now we are ready to compare this prediction for binary pulsars PSR1913+16 and PSR1534+12 with the measured values of in the two best-observed cases. Orbital quantities are taken from (Taylor et al., 1992) – see 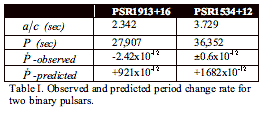Table I. The period change rate for PSR1534+12 is not yet seen, so the table shows the observational error of the measurement. At a glance, we see there is no possible match. The predicted period changes that would result if gravity propagated at the speed of light in a manner analogous to electromagnetic forces are orders of magnitude larger than the observed period changes. For PSR1913+16, they have the opposite sign as well. From PSR1534+12, we can set a lower limit to the speed of gravity as an electromagnetic-type propagating force: 2800.

We could have seen the essence of this result at the outset. Binary pulsars decay as they radiate away angular momentum, presumably in the form of gravitational radiation. However, a finite speed of propagation of gravitational force must add angular momentum to orbits. This is because the retarded position of any source of gravity must lie in the same direction relative to its true position as the tangential motion of the target body. Therefore, any delay in gravity will always pull the target in a direction that will increase its instantaneous orbital speed – the opposite of the effect of gravitational radiation.

In concluding this section, we should also note that, even in the solar system, the Sun moves around the barycenter in a path that often takes the barycenter a million kilometers or so from the Sun. So the idea that the Sun’s field can be treated as “static” and unchanging is not a good approximation even for our own planetary system. The Sun’s motion during the light time to the planets is appreciable, yet its gravity field is continually updated without apparent delay.

2. Myth: Gravitational waves contribute to gravitational force

Few subjects in physics are in such a state of confusion as is the subject of gravitational waves. Normally, this term is synonymous with gravitational radiation, a hypothetical, ultra-weak disturbance of space-time induced by a certain type of asymmetric change in the distribution of matter called a quadrupole moment. It is supposed to be analogous to accelerating charges emitting photons. This form of radiation is predicted by GR. The acceleration of binary pulsar PSR1913+16 is said to be in accord with the predicted amount of gravitational radiation, and therefore to provide an indirect confirmation of the prediction. However, attempts to detect gravitational waves in the laboratory from any source have yet to yield events that have convinced a consensus of their reality. The LIGO experiment is being designed to provide definitive detections, assuming these waves exist.

When gravitational waves were predicted, it was natural to associate them with supernova explosions, since no known event in nature redistributes mass in space more rapidly. However, the explosion must be asymmetric to produce gravitational waves. Because the gravitational field of the supernova is changing rapidly during the explosion, it is natural to associate the production of gravitational waves with changes in gravitational fields. So far, so good.

However, many physicists do more than associate the two concepts, and consider that changes in gravitational fields are gravitational waves. The heart of this confusion is illustrated by the following passage from (Synge, 1960): “Suppose that a man, standing on the earth, holds in his hand a heavy club. At first the club hangs down toward the ground, but at a certain moment the man raises it quickly over his head. Any theory of gravitation recognizes that the club produces a gravitational field, however minute it may be, and that the action of the man changes that field, not only in his neighborhood, but throughout the whole universe. According to Newtonian theory, the effect is instantaneously felt on the moon, on the sun and in every remote nebula. Since we are not concerned with Newtonian theory, we do not have to discuss the absurdity of this. As relativists, familiar with the idea that no causal effect can travel faster than light, ..., we would guess that the change in the gravitational field of the moving club travels out into space with the speed of light. And we would call this moving disturbance a gravitational wave. Thus, on a very general basis, we must regard the physical existence of gravitational waves, so understood, as self-evident.”

The sudden displacement of the club may cause a disturbance of space-time, which would be a form of gravitational radiation. Separately, if gravitation is itself some sort of wave phenomenon, changes in gravitational fields will propagate away from a source as waves. Now there is no doubt that changes in gravitational fields exist, or that they can be detected in the laboratory. Therefore, this phenomenon cannot be the same thing as gravitational radiation, since the latter has not yet been reliably detected, and its existence still remains unverified. However, both phenomena are called “gravitational waves” without further distinction. For the former type, we must look to ultra-small accelerations of distant, massive pulsars for some hint of their existence. For the latter type, we see indirect evidence of changes in the gravitational fields of Sun and Moon every day in the tides, or can measure them directly with a gravimeter. We can even measure gravitational field changes using small masses in a purely laboratory setting.

The consequences of this distinction become clearer when we are careful to distinguish sources and targets of gravity. Ordinary gravitational acceleration of a target results from some form of communication from a source of gravity that may or may not be carried from source to target in wave form. Separately, the acceleration of a target body must change the nearby space-time, and such changes seem likely to be propagated outward in wave form away from the target. If possible waves associated with sources of gravity (those that may induce acceleration in other bodies), and other possible waves induced by targets of gravity (those that result from acceleration), are not distinguished, we are certain to have massive confusion over the meaning of the very concept of “the speed of gravity”.

In a binary pulsar, where both masses are comparable, both stars may emit gravitational radiation. But each would do so as a consequence of its acceleration induced by the other, not as a consequence of its own gravity. Moreover, as we noted earlier, gravitational waves in the sense of gravitational radiation cause orbiting bodies to lose angular momentum; whereas gravitational aberration that must accompany any finite speed of propagation of gravity from a source to a target would cause orbits to gain angular momentum.

Therefore, it seems fairly certain that, if gravitational radiation exists, its waves will propagate at the speed of light. In what way this type of disturbance of space-time may differ from very-long-wavelength electromagnetic disturbances of space-time, if indeed it does differ, remains to be seen.

By contrast, the speed of propagation of gravitational fields and of changes in those fields, whatever the nature of the propagating agents, are different matters, and pose a question we hope to answer in this paper.

Space-Time Curvature and Retarded Potentials

1. Is gravity caused by a curvature of space and time?

A common way to explain why gravity can appear to act instantaneously, yet still propagate with a delay, is the rubber sheet analogy. (See Figure 4.) A large mass sitting on a rubber sheet would make a large indentation, and that indentation would induce smaller nearby masses to role toward the indentation. This is an analogy for curved space-time, which is likewise supposed to be the cause of bodies accelerating toward large masses. The reasoning in the analogy further suggests that target bodies simply respond instantly to the local curvature of the underlying space-time medium (like the rubber sheet). Therefore, any delay associated with altering that local curvature would not produce aberration, and the target body would appear to respond instantaneously to the source unless the source suddenly changed its motion.

The rubber sheet analogy is represented as a way of visualizing why bodies attract one another. However, in that regard, it is highly defective. A target body sitting on the side of an indentation would stay in place, with no tendency to roll downhill, unless there were already a force such as gravity underneath the rubber sheet pulling everything downhill. And this failure of the analogy helps us identify the precise problem with the curved space-time description of gravity – the lack of causality. Without consideration of why a target body is induced to accelerate through space, and how quickly it receives updates of information about how to accelerate through space, neither the space-time curvature explanation nor the rubber sheet analogy can help us understand why gravity appears to act so much faster than light.

Moreover, contrary to what the rubber sheet analogy implies, an orbiting body such as a spacecraft orbiting the Earth is not following the curvature of space near the Earth. As we remarked earlier, two spacecraft some distance apart in the same orbit could stretch a tether between them and pull it taut, thereby describing a straight line through space different from their orbital path. In more mathematical terms, the supposed curvature of space-time produced by a gravitational field is an effect proportional to the local gravitational potential , the variable part of which is in turn proportional to , where is orbital speed. Yet, orbital curvature through space, like stellar aberration, is proportional to , a much larger effect. For example, for the Earth orbiting the Sun, is of order 10^-4, and is of order 10^-8. So we see that almost all of the acceleration of bodies through space is not a consequence of the curvature of space. In the GR explanation, the acceleration through space is due to the curvature of “space-time”, a mathematical entity not to be confused with the combined separate concepts of space and time.

While relativists have always been partial to the curved space-time explanation of gravity, it is not an essential feature of GR. Eddington (1920, p. 109) was already aware of the mostly equivalent “refracting medium” explanation for GR features, which retains Euclidean space and time in the same mathematical formalism. In essence, the bending of light, gravitational redshift, Mercury perihelion advance, and radar time delay can all be consequences of electromagnetic wave motion through an underlying refracting medium that is made denser in proportion to the nearness of a source of gravity. (Van Flandern, 1993, pp. 62-67 and Van Flandern, 1994) And it is now known that even ordinary matter has certain electromagnetic-wave-like characteristics. The principal objection to this conceptually simpler refraction interpretation of GR is that a faster-than-light propagation speed for gravity itself is required. In the context of this paper, that cannot be considered as a fatal objection.

Lastly, we note experimental evidence from neutron interferometers that purports to demonstrate a failure of the geometric weak equivalence principle, that gravity is due to a curvature of space-time. (Greenberger & Overhauser, 1980) This experiment confirmed the strong equivalence principle (local equivalence of a uniform acceleration and a gravitational field), but its results are incompatible with the geometrical weak equivalence principle because interference effects in quantum mechanics depend on the mass. This is because the wave nature of the neutron depends on the momentum of the neutron, which is mass times velocity. So all phase-dependent phenomena depend on the mass through the wavelength, a feature intrinsic to quantum mechanics.

Since the experiment confirms the applicability of quantum mechanics even in the presence of gravity, including this non-geometrical mass dependence, the experiment seems to be a step in the undermining of the purely geometrical point of view, and “tends to bother theorists who prefer to think of gravity as being intrinsically related to geometry”, according to the authors.

2. Does GR really reduce to Newtonian gravity in low-velocity, weak-field limit?

As we have already noted, Newtonian gravity propagates with unconditionally infinite speed. How, then, can GR reduce to Newtonian gravity in the weak-field, low-velocity limit? The answer is that conservation of angular momentum is implicit in the assumptions on which GR rests. However, as we have already seen, finite propagation speeds and conservation of angular momentum are incompatible. Therefore, GR was forced to claim that gravity is not a force that propagates in any classical sense, and that aberration does not apply.

In practice, this suppression of aberration is done through so-called “retarded potentials”. In electromagnetism, these are called “Lienard-Wiechert potentials”. For examples of the use of retarded potentials, see (Misner et al., 1973, p. 1080) or (Feynman, 1963, p. 21-4). Suppose we let be the gravitational potential at a field point and time , be the gravitational constant, be an element of volume in the source of the potential, be the coordinates of that volume element in the source, be the matter density at point and time , , be the distance from the source volume element at time to the field point at time , and be the relative velocity between the field point and the source. Then two different forms of retarded potentials in common use for gravitation are these:

[3]

[4]

In [3], we have used as the retarded time. Then the triple integral evaluates the density one light time ago in place of the present density, as might be useful if a non-spherically symmetric source body were rotating. In [4], the mutual distance is taken to depend on the scalar distance of the source one light time ago.

However, in neither form of retarded potential is any consideration given to the transverse motion between source and target during the light time; i.e., the aberration. Ignoring aberration is logically equivalent to adopting an infinite propagation speed for gravitational force. That point is glossed over by emphasizing that the density distribution or the mutual distance is being taken at its retarded position, as if a finite propagation speed for gravity were being adopted. Nevertheless, the only practical consequence of a finite propagation speed that matters in most applications is missing from these potentials. And that clever trick then allows a theory with “gravity propagating at the speed of light” to be equivalent to a theory with infinite propagation speed in the weak-field, low velocity limit.

In short, both GR and Newtonian gravity use infinite propagation speeds with aberration equal to zero. In Newton’s laws, that fact is explicitly recognized even though aberration and delay terms do not appear because of an infinity in their denominator. In GR, much effort has been expended in disguising the continued absence of the same delay terms by including retardation effects in ways that are presently unobservable and ignoring aberration. Every physicist and physics student should be at least annoyed at having been tricked by this sleight of hand, and should demand that the neglect of aberration be clearly justified by those who propose to do so.

Does a Gravitational Field Continuously Regenerate, or is it “Frozen”?

In attempts to describe how GR can affect distant bodies seemingly without delay, relativists often speak of the field of a body as if it were a rigid extension of the body itself. If such a “static” field has no moving parts, it then would have no need of a propagation speed unless something changes. The objection to this picture is that it is acausal. Somehow, momentum is transferred from a source body to a target body. It seems impossible to conceive of a static field with literally no moving parts as capable of transferring momentum. This is the dilemma of the “rubber sheet” analogy again. Just because a rubber sheet or space-time is curved, why should a stationary target body on the slope of such a curve begin moving toward the source? What is the source of the momentum change?

To retain causality, we must distinguish two distinct meanings of the term “static”. One meaning is unchanging in the sense of no moving parts. The other meaning is sameness from moment to moment by continual replacement of all moving parts. We can visualize this difference by thinking of a waterfall. A frozen waterfall is static in the first sense, and a flowing waterfall is static in the second sense. Both are essentially the same at every moment, yet the latter has moving parts capable of transferring momentum, and is made of entities that propagate.

As this applies to gravitational fields for a fixed source, if the field were static in the first sense, there would be no need of aberration, but also no apparent causality link between source and target. If the field were static in the second sense, then the propagation speed of the entities carrying momentum would give rise to aberration; and the observed absence of aberration demands a propagation speed far greater than lightspeed.

So are gravitational fields for a rigid, stationary source frozen, or continually regenerated? Causality seems to require the latter. If such fields are frozen, then what is the mechanism for updating them as the source moves, even linearly? Even a “rigid” bar pushed at one end would not move at the other end until a pressure wave had propagated its entire length. Moreover, we seem to need two mechanisms – one to curve space-time when a mass approaches, and another to unbend it when the mass recedes. This is because, once a curve is “frozen” into space-time, it will not necessarily “melt” back to its original condition when the cause is removed. Yet, there is no available cause for either process to result from a field with no moving parts.

We can also deduce the consequences for a source in continual acceleration, such as the Sun in our solar system. The Sun’s path around the solar system barycenter induced by planetary perturbations causes excursions of over a million kilometers, and the barycenter is sometimes outside the physical body of the Sun. So the Sun’s field must be continually updated at all distances to infinity. Surely, this updating requires the propagation of causal agents from the source. And since the source is continually accelerating, the regeneration of the distant field must likewise be a continuous process, requiring propagation. However, propagation involves delays, and even in the solar system, we have observationally ruled out delays as great as lightspeed propagation would produce. For example, the solar eclipse experiment is sensitive to delays in the continual updating of the Earth’s field by the Sun as they both affect the Moon, and update speeds of at least 20are required.

The binary pulsar experiment provides another, more direct demonstration that even changes in gravitational fields must propagate faster than light. Ultimately, GR proposes that such changes appear to act instantaneously in the “near field”, but eventually show their true, light-speed-delayed character in the “far field”, which is conveniently beyond our present ability to observe. The necessity of this dual behavior is to prevent the logical need for changes to continue to appear to act instantaneously at ever increasing distances, even to infinity.

However, this only prevents certain types of paradoxes from arising. When the subject of “black holes” first comes up in physics classes, a frequently asked question is “If nothing can escape the event horizon because nothing can propagate faster than light, how does gravity get out of a black hole?” The answer usually provided is that the field around a black hole was frozen into the surrounding space-time prior to the collapse of the parent star behind an event horizon, and has remained in that state ever since. By implication, there is no need for continual regeneration of the external field by causal agents from the source.

However, let us suppose we have a binary black hole, with the two collapsed stars in elliptical orbits around one another. See Figure 5. Then each field must be continually updated by a changing contribution from the orbiting field of the other. How does each field know what it is supposed to do if it is no longer in communication with its source mass hidden behind an event horizon? If the curvature of space-time at a point near black hole A becomes zero because black hole B is equally distant, what makes it non-zero again once black hole B recedes?

Indeed, if each source mass is forced to accelerate, why should each field point with a certain curvature undergo exactly the same acceleration as the source, making the whole field (to infinity?) appear frozen rigidly to the parent black hole? Perturbations by the other star are different at every different field point, so each such space-time field point should experience a different acceleration. With no communication, how can the whole system remain intact and coherent?

We conclude that the concept of frozen gravitational fields is acausal and paradoxical. Gravitational fields must continually regenerate, like a flowing waterfall. In doing so, they must consist of entities that propagate. And the speed of propagation of those entities must greatly exceed the speed of light.

Conclusion: The Speed of Gravity is ³ 2x10¹⁰

We conclude that gravitational fields, even “static” ones, continually regenerate through entities that must propagate at some very high speed, . We call this the speed of gravity. Equation [1] then tells us how orbits will expand in response to this large but finite propagation speed, since the field itself, and not merely changes in the field, will transfer momentum to orbiting target bodies. Rewriting equation [1] in a form suitable for comparisons with observations, we derive:

[5]

For the Earth’s orbit, = 1 year, = 10^-4, and we take as an upper limit to the value 2.4x10^-12/year (derived from ½ ) in solutions using radar ranging and spacecraft data (Pitjeva, 1993). Substituting these values, we get from Earth-orbit data that ³ 10⁹.

Using the same equation with binary pulsar PSR1534+12 and the parameters in Table I, we can place the most stringent limit yet from the observed uncertainty in : ³ 2x10¹⁰.

A direct experimental verification in the laboratory that gravity propagates faster than light may now be possible. The protocol and preliminary results were reported in (Walker, 1997).

It might be tempting to conclude that the speed of gravity is infinite. But these limits on are still a long way from infinite velocity, and Newton’s statement, quoted at the beginning of this paper, still seems applicable. Infinite speeds, too, are acausal.

Consistency with Special Relativity

Einstein special relativity (SR) is able to prove based on its premises that nothing can propagate faster than the speed of light in forward time. Is our result for the speed of gravity an experimental falsification of SR? The correct answer must be a qualified “yes and no”. Strictly, the minor new interpretation of SR needed for consistency with our result is no more a falsification of SR than GR was a falsification of Newtonian gravity. In both cases, the earlier theory was incomplete rather than wrong. We will now examine exactly what must change about SR for full consistency with all existing experimental evidence and this new result as well.

A brief overview of the history of relativity will provide useful background for this section, since everything proposed here has been proposed before. The “principle of relativity”, that the laws of physics should be the same as viewed from any inertial frame, dates to the 19^th century, well before it was popularized by H. Poincare. The well known “Lorentz transformations” embody that principle, but were not original when Lorentz adopted them for his own theory of relativity, first published in 1904 in an “aether” context. Einstein’s main contribution with his famous 1905 paper, then, was the addition of a second postulate, that the speed of light will be locally the same for all observers regardless of their own state of motion. This did away with the need for an aether, or more generally, with a preferred frame of reference.

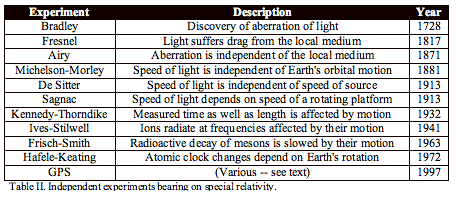
The ensuing years saw much discussion of whether nature was more like Einstein’s SR or Lorentzian relativity (LR). The experiments relevant to testing relativity are listed in Table II. The discovery of Fresnel drag had seemed at first to demand the existence of an aether, but relativists eventually found ways to explain it using SR too. The Airy water-filled telescope experiment showed that the aberration of starlight was unchanged by passing through a water medium even though that medium slowed the speed of light by about 30%. This too seemed to favor the existence of a preferred frame because the local speed of light did not affect aberration, showing that aberration was determined outside the telescope rather than by the conditions most local to the observer. However, Einstein supporters could also explain this result using SR, albeit with somewhat more complexity.

The Michelson-Morley experiment is the first (and only) observation that seemed to strongly favor SR over LR, although Michelson himself never accepted that. The expected aether-drift speed did not put in an appearance in the test results, and the speed of light did indeed seem to be the same in all directions, as SR postulated, even though the observer was obviously moving at high speed in some direction through space. It was not until the last decade that serious consideration was given to the possibility that the local gravity field may always constitute a preferred frame. This idea was popularized in (Beckmann, 1987) and then widely discussed in the journals Galilean Electrodynamics <http://msx2.pha.jhu.edu/~dring/gehtmls/gehome.html> and Apeiron <http://redshift.vif.com/default.htm>, and occasionally in the Meta Research Bulletin <http://www.metaresearch.org>.

It is now well-established that LR is fully compatible with the Michelson-Morley experiment, and in general with the expectation that the speed of light will seem to be the same even when the observer is moving provided that certain conditions are met, although not under all circumstances. That the speed of light is independent of the speed of its source is unremarkable, since that is a property of all wave motion. However, being independent of the speed of the observer is special. Choosing to synchronize clocks using the Einstein convention automatically makes one-way speed of light independent of the speed of the observer because that assumption is built into the Einstein synchronization method. If some other convention were used to synchronize clocks, such as synchronizing them to an underlying common inertial frame (as is done for the Global Positioning System satellites, or when astronomers synchronize phenomena to a barycentric frame using time provided by distant pulsars), then the one-way speed of light would be different in each direction when measured by observers moving with respect to that special frame. The round-trip speed of light uses a single clock to measure elapsed time, and so does not depend on synchronization. But if the rate of an ordinary clock is affected by its speed in a Lorentzian way, which we now know to be the case, then the measured speed of light will appear to be an invariant in all directions. Using a clock whose rate is not affected by its translational speed, for example pulses in the strength of the gravitational field from a compact, massive binary star, would apparently allow the speed of the observer relative to the local mean gravity field to be detected.

Following the publication of Einstein’s SR paper, two new experimental results were published in 1913, both favoring LR over SR. Indeed, Sagnac claimed a falsification of SR on the grounds that the local speed of light was affected by observer velocity if the observer was attached to a rotating platform. He showed that the Michelson-Morley experiment performed in such a rotating frame did show fringe shifts, and concluded that, even if linear motion was relative, rotational motion was absolute. DeSitter noted that stellar aberration was the same for both components of distant binary stars, even though the relative velocity of each with respect to the observer was quite different. Therefore velocity in some special frame (we might now say velocity in the local gravity field relative to the distant gravity field) rather than relative velocity between source and observer determines aberration. Both of these experiments were blows to SR’s contention that all motion was relative. Nonetheless, SR supporters came up with explanations of these phenomena too in an SR context, and these fairly non-trivial explanations are the subjects of textbooks on relativity today.

The Michelson-Gale experiment of 1925 involving the same Michelson as in the Michelson-Morley experiment again claimed a contradiction of SR – a theory that Michelson never found acceptable. History has concluded that this experiment is essentially another demonstration of the Sagnac effect, and no longer cites it as a significant independent experiment; so it is omitted from our table. Ives and Stilwell (1938) drew conclusions similar to those of Michelson, and specifically argued that their own experiment confirmed LR (which they called the Larmor-Lorentz theory) over SR. Yet today, it is simply added to the list of SR-confirming experiments.

When the muon lifetime experiments were performed in the 1960s, LR had been all but forgotten. Questions were raised briefly about whether the situation was reciprocal – whether high-speed muons would really see laboratory muons live longer. SR offered assurance that they would, but no test was then possible. By the time the Hafele-Keating experiment compared traveling atomic clocks sent around the world in opposite directions with a stay-at-home clock, an experiment later improved upon by C.O. Alley at the Univ. of Maryland, it was no longer considered remarkable that the velocity effects on clocks had to be based on speeds in the underlying inertial frame instead of the relative velocities of the clocks.

Finally, the Global Positioning System (GPS) showed the remarkable fact that all atomic clocks on board orbiting satellites moving at high speeds in different directions could be simultaneously and continuously synchronized with each other and with all ground clocks. No “relativity of simultaneity” corrections, as required by SR, were needed. This too seemed initially to falsify SR. But on further inspection, continually changing synchronization corrections for each clock exist such that the predictions of SR are fulfilled for any local co-moving frame. To avoid the embarrassment of that complexity, GPS analysis is now done exclusively in the Earth-centered inertial frame (the local gravity field). And the pre-launch adjustment of clock rates to compensate for relativistic effects then hides the fact that all orbiting satellite clocks would be seen to tick slower than ground clocks if not rate-compensated for their orbital motion, and that no reciprocity would exist when satellites view ground clocks.

Why then did SR win out over LR? Three circumstances conspired to make SR appear to be the better solution to describing nature in the early years of the 20^th century. (1) Classical thinking about the aether almost always involved a universal field rather than a local field. No one took seriously that each local gravity field might serve as a preferred frame for local observers. Yet that now seems the case. (2) The wave nature of matter had not yet been discovered by deBroglie. Before that happened, there was no logical reason to expect that clocks based ultimately on atomic oscillations would have their rates affected by observer motion in the same way that the speed of light would be affected by observer motion, rendering observer motion undetectable in experiments. However, that also now seems to be true (Van Flandern, 1993, p. 72-77). (3) The success of GR in predicting the light-bending effect at the 1918 solar eclipse gained great credibility for GR, and SR benefited from this success because it was widely believed that GR was based on SR. But GR is usually implemented using a preferred frame closely coinciding with the local gravity field, with the consequence that only the features that SR and LR have in common were integrated into GR. The reciprocity of time dilation between two inertial frames, a key way in which SR differs from LR, plays no role in GR.

The principal differences between the two relativity theories stem from the equivalence of all inertial frames in SR, and the existence of a preferred frame in LR. Otherwise, SR’s time dilation is equivalent to LR’s clock slowing; SR’s space contraction is equivalent to LR’s meter-stick shrinkage; and SR’s change in the momentum of moving bodies is equivalent to LR’s. However, LR recognizes a “universal time” apart from the time kept by electromagnetic-based clocks affected by motion. And the law of addition of velocities between two frames, neither of which is the preferred frame, is different in LR than in SR. For a derivation of this law and the revised form of the Lorentz transformations for Lorentzian universal time, see (Mansouri & Sexl, 1977). For our purposes here, we simply note that the proof that nothing can propagate faster than the speed of light in forward time does not apply to LR.

Near the end of his career, Lorentz is quoted as having graciously conceded the contest: “My theory can obtain all the same results as special relativity, but perhaps not with a comparable simplicity.” (private communication from C.O. Alley) Today, with hindsight, we might make a somewhat different assessment: “Special relativity can explain all the experimental results in Table II that Lorentzian relativity can, but perhaps not with a comparable simplicity.” Even so, SR cannot explain the faster-than-light propagation of gravity, although LR readily can.

We conclude that the speed of gravity may provide the new insight physics has been awaiting to lead the way to unification of the fundamental forces. As shown in (Van Flandern, 1993, pp. 80-85 and Van Flandern, 1996), it may also be connected with the explanation of the dark matter problem in cosmology. Moreover, the modest switch from SR to LR may correct the “wrong turn” physics must have made to get into the dilemma presented by quantum mechanics, that there appears to be no “deep reality” to the world around us. Quantum phenomena that violate the locality criterion may now be welcomed into conventional physics.

Acknowledgments

The author is indebted to numerous correspondents who have challenged the conclusions of this paper in so many different ways, especially in USENET discussion groups such as sci.physics, sci.physics.relativity and sci.astro. Each of these challenges has forced a new and deeper investigation, without all of which the present paper could never have hoped to pass peer review. One relativist in particular, Steve Carlip of UC Davis, had the patience to stay with this issue over a span of several years, defending the GR interpretation to the fullest extent possible. Between us we have written enough prose, created enough analogies, pondered enough equations, and consulted enough references to fill a book.

The author further thanks Jeffery Kooistra for his key role. His Analog article (Kooistra, 1997) flushed this subject to the forefront once again, and his inquiries to both Steve Carlip and to the author forced us to explain our positions in layman’s language, and thereby diverted us from talking past one another. Discussions with colleagues too numerous to mention must likewise be acknowledged. But Jean-Pierre Vigier, in addition to several penetrating questions, encouraged the author to stop talking and start writing, promising a fair peer review process at the conclusion. Without such encouragement, this paper would certainly not have come into existence.

[Final version published: Physics Letters A 250:1-11 (1998); also: Infinite Energy 5 #27:50-58 (1999).

See published comment: G.E. Marsch, C. Nissim-Sabat, “Comments on ‘The speed of gravity’”, Phys.Lett.A 262:103-106 (1999).

See response: T. Van Flandern, “Reply to comments on ‘The speed of gravity’”, Phys.Lett.A 262:261-263 (1999).

See additional comment: S. Carlip, “Aberration and the speed of gravity”, Phys.Lett.A 267:81-87 (2000).

See response to above and all other comments: “Experimental Repeal of the Speed Limit for Gravitational, Electrodynamic, and Quantum Field Interactions”, T. Van Flandern and J.P. Vigier, Foundations of Physics 32:1031-1068 (2002).

As of 2006/02/04, no further comment or criticism has appeared.]

Bibliography

Beckmann, P., Einstein Plus Two, Golem Press (1987).

Danby, J.M.A., Fundamentals of Celestial Mechanics, Willmann-Bell, Richmond, VA (1988).

Eddington, A.E., Space, Time and Gravitation, original printed in 1920, reprinted by Cambridge Univ. Press, Cambridge (1987).

Feynman, R.P., Leighton, R.B. and Sands, M., The Feynman Lectures on Physics, Vol. II, Addison-Wesley, Reading, Mass. (1963).

Greenberger, D.M. and Overhauser, A.W., “The role of gravity in quantum theory”, Sci.Amer. 242 (May):66-76 (1980).

Hoffman, B., Relativity and its Roots, Freeman, New York, NY (1983).

Kooistra, J.D., “Paradigm shifty things”, Analog CXVII #6:59-69 (1997).

Ives, H.E. and Stilwell, G.R., “An experimental study of the rate of a moving atomic clock”, J.Opt.Soc.Amer. 28#7:215-226 (1938).

Laplace, P., Mechanique Celeste, volumes published from 1799-1825, English translation reprinted by Chelsea Publ., New York (1966).

Mansouri, R. and Sexl, R.U., “A test theory of special relativity: I. Simultaneity and clock synchronization”, Gen.Rel.&Grav. 8:497-513 (1977).

Misner, C.W., K.S. Thorne & J.A. Wheeler, Gravitation, W.H. Freeman & Co., San Francisco, CA (1973).

Pitjeva, E.V., “Experimental testing of relativity effects, variability of the gravitational constant and topography of Mercury surface from radar observations 1964-1989”, Cel.Mech.&Dyn.Astron. 55:313-321 (1993).

Synge, J.L., Relativity, North-Holland Publishing Co., Amsterdam, Ch. IX (1960).

Taylor, J.H., Wolszczan, A., Damour, T. & Weisberg, J.M., “Experimental constraints on strong-field relativistic gravity”, Nature 355:132-136 (1992).

Van Flandern, T., Dark Matter, Missing Planets and New Comets, North Atlantic Books, Berkeley, CA (1993).

Van Flandern, T., “Relativity with Flat Spacetime”, MetaRes.Bull. 3:9-13 [see <http://www.metaresearch.org>] (1994).

Van Flandern, T., “Possible new properties of gravity”, Parts I & II, MetaRes.Bull. 5:23-29 & 38-50 [see <http://www.metaresearch.org>] (1996).

Walker, W.D., “Superluminal propagation speed of longitudinally oscillating electrical fields”, abstract in Causality and Locality in Modern Physics and Astronomy: Open Questions and Possible Solutions, S. Jeffers, ed., York University, North York, Ontario, #72 (1997).